Partial quotients division with a number to 100
Students learn partial quotients division with a number to 100.


8,000 schools use Gynzy
92,000 teachers use Gynzy
1,600,000 students use Gynzy
General
The students learn partial quotients division with a number to 100.
Standards
CCSS.Math.Content.5.NBT.B.5
Learning objective
Students will be able to solve partial quotients with a number to 100.
Introduction
On the interactive whiteboard there are several division problems that the students must solve. This includes problems with and without visual support. A story problem is also included.
Instruction
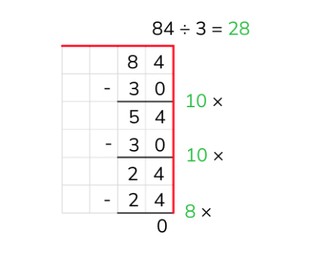
Explain that with partial quotients division you break up the problem into steps and solve it in this way. You write down the problem and draw a line underneath it. Next you can make a helping row of the table of the number that you are dividing by. You don't have to include every problem in this row. For example, you can always double or halve the problems. After that you solve the problem step by step and see how many times 3 fits in 66. After every step you write down how much you have left over. If you do not have any more left over, then you have finished. You then add up all of the numbers that tell how many times 3 fits in 66 (10, 10, and 2). Have the students solve more problems using partial products. Have them write down the problems on graphing paper, and also write down the table of the divisor if they need to. Next you explain that you can also solve a problem with larger numbers in the same way. The students also practice this kind of problem. Ask various students what steps they took to solve the problems. Encourage the students to take as large steps as they can.
Check whether the students can divide using partial products by asking the following questions:
- Why is it useful to be able to divide using partial products?
- What aid can you use when dividing using partial products?
- Solve this problem using partial products division: 72 ÷ 12
Quiz
The students test their understanding of partial products division with a number to 100 through ten exercises. For these exercises they can write out the problem and the intermediate steps on graphing paper. They can also write down the table of the divisor if they need to. Some of the exercises are with larger numbers.
Closing
You discuss once again with the students that it is important to be able to divide using partial products with a number to 100, because that is how you can solve division problems in an easier way. Check whether the students know that with partial products division you take steps to solve pieces of the problem and that they can make a helping row to help them with their calculations. Have the students solve a number of problems using partial products division. Next they explain in pairs to their parter how they solved the problem. Did they do the same steps?
Teaching tips
When students have difficulty with partial products division, you can have them make helping rows of the table of the number that they are dividing by. Have them solve a problem step by step. Pay attention to each of the steps that the students take and try to encourage them to take the largest steps that they can (not 10 × 3 = 30 and 10 × 3 = 30, but in one step 20 × 3 = 60).
Instruction materials
Graphing paper
The online teaching platform for interactive whiteboards and displays in schools
Save time building lessons
Manage the classroom more efficiently
Increase student engagement
Discover more!
About Gynzy
Gynzy is an online teaching platform for interactive whiteboards and displays in schools.
With a focus on elementary education, Gynzy’s Whiteboard, digital tools, and activities make it easy for teachers to save time building lessons, increase student engagement, and make classroom management more efficient.